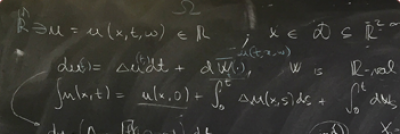
Complex Analysis: theory of approximations by analytic and harmonic functions, best approximations; applications of uniform and tangential approximations in various fields of complex analysis; investigation of problems of Weierstrass theory of analytic functions; Banach algebras of analytic functions; uniqueness problems of analytic and harmonic functions; value distribution theory of analytic and meromorphic functions; boundary value theory and boundary behavior of analytic, harmonic and subharmonic functions; integral transformations theory in complex domain; integral representations and classes of analytic and harmonic functions in multidimensional domains.
Real Analysis: trigonometric and general orthogonal series; bases in functional spaces; weighted functional spaces; differentiation of multidimensional integrals; representation and uniqueness for multiple Haar, Franklin, Walsh and trigonometric series; nonlinear approximation.
Probability Theory: integral and stochastic geometry; combinatorial integral geometry; point processes; sections of convex bodies by random planes and lines; measures generation by finite additive functionals; mathematical problems of statistical physics; limit theorems for random Gibbs processes and fields; statistics of stationary Gaussian processes.
Differential and Integral Equations: methods and algorithms for solution of equations; accelerating the convergence of decompositions by eigenfunctions of boundary problems and asymptotic estimates of the corresponding errors; computer realization of integral transforms and applications; parallelization of computations.
Mathematical Physics: methods of study and effective numerical-analytical solution of integral, integral-differential and other equations, arising in direct and inverse problems of radiative transfer, kinetic theory of gases, renewal stochastic processes, semi-Markov processes, filtration of stochastic processes, non-local interaction of waves; development of method of nonlinear factorization equations, Ambartzumian equation method; fixed point principles in the critical case.


